18 May 2017
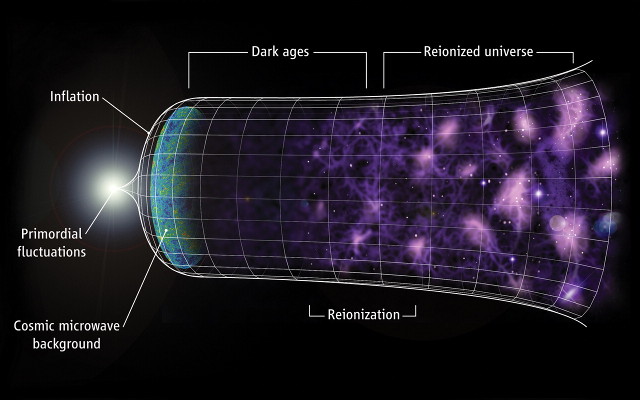
Since a couple of months we can witness an extremely interesting situation (I would rather call it a conflict) in Cosmology. A little bit of recent history. The cosmic inflation is an extremely short (about 10^{-33} seconds) period of the extremely fast Universe expansion right after the initial singularity. On 17th of March 2014 BICEP2 collaboration announced that their experiment detected the so-called B-modes. This was considered as a major evidence to support the ideas of cosmic inflation. However, on the 19th September 2014 Planck experiment showed that the results of BICEP2 were insignificant:
- Once the “galactic emission” [dust] is correctly subtracted, there still remains an excess [signal] but it is at present too weak to be considered a detection and could be the result of [experimental error].
Despite this public press release, Guth, Linde and Starobinsky were awarded in 2014 the $1 million Kavli Prize in Astrophysics…
Two months ago an interesting article by Anna Ijjas, Paul J. Steinhardt and Abraham Loeb appeared in Scientific American. This article further challenged the evidences behind cosmic inflation theory. The fact of questioning provoked violent reactions from inflation proponents including Guth and Linde. A rebuttal signed by 33 physicists appeared on Scientific American web site. On the other hand, Ijjas, Steinhardt and Loeb presented their informative rebuttal as well. This story is developing very quickly and I hope that the good science and the scientific rigour will win after all.
17 May 2017
This is post is going to be mainly the overview of various preprints that we submitted recently with my precious co-authors.
Water waves
Let us start with my favourite topic - the water waves. With Didier Clamond we finalized our preprint on the brand new regularized shallow water (Airy-Saint-Venant) equations. The main idea is to suppress shock waves (i.e. replace them by smoother fronts) without adding any dissipation, any dispersion. We decided to call this type of modification as Hamiltonian regularization. More details can be found in our preprint:
A few days ago I delivered a colloquium talk on this topic at the Laboratoire de Mathématiques Raphaël Salem, University of Rouen. The slides can be downloaded here.
Stratified flows
Last month with Valery Liapidevskii we finalized a work, which was started back in 2011 when Valery came to my university as invited Professor. This work is devoted to the modelling of turbidity (density) currents in general, and focuses especially on the determination of the front velocity. After so many years of collaboration, the article turned out to be quite long:
Building physics
And as always, there is a number of new submissions on the building physics matters. First of all, we continued our researches on the identification and optimal experimental design:
This is already the third preprint in this direction. Moreover, we started a new research direction - the application of spectral methods to building physics. The spectral methods are not new. However, they seem to be essentially unknown in the building physics community. Moreover, they are so efficient that they can be seen as model reduction techniques. Two following preprints are devoted to this topic:
- S. Gasparin, J. Berger, D. Dutykh & N.Mendes. Spectral Methods - Part 1: A fast and accurate approach for solving nonlinear diffusive problems, 40 pp., Submitted, 2017
- S. Gasparin, J. Berger, D. Dutykh & N. Mendes. Spectral Methods - Part 2: A comparative study of reduced order models for moisture transfer diffusive problems, 36 pp., Submitted, 2017
Nota bene:
It goes without saying that all preprints are freely available through HAL server. The links are provided above.
08 Apr 2017
Recently we submitted a couple of manuscripts, which report on our progress in the development of new numerical approaches for future building simulation’ tools.
The first preprint is basically the generalization of the Dufort-Frankel method applied earlier to scalar nonlinear models. This time we go to coupled nonlinear heat and moisture transfer. Moreover, we apply our algorithms to realistic configurations of two adjacent rooms together with air temperature inside. So, these results are described in this preprint together with the advantages of using explicit schemes to avoid synchronisation problems and large coupled nonlinear systems:
The second preprint is rather a continuation of our previous investigation on the optimal experimental design. This time we consider more general models including also some advection effects of moisture and we solve an inverse problem to estimate material properties. The experimental part of this work was brilliantly performed by Thomas Busser:
That’s all for the moment. More preprints are coming in the nearest future.
28 Feb 2017
From 20th to 25th of February 2017 I participated in a workshop organized by the Faculty of Mechanics and Mathematics of the Al-Farabi Kazakh National University. The goal of this workshop was mainly to discuss a new Bachelor degree Programme Applied and Computational Mathematics. The particularity of this Programme is that all courses are going to be taught in English. This educational programme is a part of the “Kazakhstan 2050” Strategy.
Among the participants (besides the Author of this post) we had the pleasure to count the following experts:
- Sergey Cherny, Institute of Computational Technologies, SB RAS, Russia
- Alexander Gasnikov, Moscow Institute of Physics and Technology, Russia
- Sergey Kabanikhin, Institute of Computational Mathematics and Mathematical Geophysics, SB RAS, Russia
- Julius Kaplunov, Keele University, UK
- Matthias Meinke, RWTH Aachen, Germany
- Lian-Ping Wang, University of Delaware
The conclusions and recommendations issued during this workshop are going to be published in workshop materials to make outcomes available for other Kazakh (and not only Kazakh) Universities.

15 Feb 2017
There are many points to mention and describe briefly today.
First of all, together with my collaborator Didier Clamond, we submitted a manuscript, which describes a new method for the computation of cnoidal waves in the full Euler equations with free surface:
These solutions can be used to validate and check the accuracy of various dynamic solvers for the full water wave problem. Moreover, the Matlab code is freely available at this URL:
This Matlab code computes irrotational 2D periodic steady surface pure gravity waves of arbitrary length in arbitrary depth. The formulation is based on the so-called Babenko equation and pseudo-spectral discretization in the conformal domain. The resulting equation is solved using Petviashvili iteration method.
In the continuation of our previous short publication on peaked solitary capillary-gravity waves, we submitted the full manuscript, which investigates this system of equations (capillary-gravity Serre model) in more details:
In the last manuscript we focus more on the dynamics and properties of smooth solitary wave solutions in various regimes with respect to the Bond number.
Finally, the following week I am going to spend at Al-Farabi Kazakh National University



